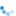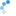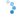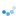杨昌周
(甘肃省永靖县刘家峡中学,甘肃 永靖)
摘 要:深度学习是培养学生自主学习能力的重要方式 。深度学习能够引导学生深入挖掘知识,掌握有效能力,是新时代课堂教 学的新手段。而学生是学习的主体,是课堂的主要参与者,正确认识学生的角色和地位,才能够更好地发挥学生的学习能动性,让他们 更加自主地去学习和实践。由此,在初中数学教学中,教师应当积极探索深度学习手段,以有效的方式构建高效的课堂,提升学生的学 习能力与教学效率,完善深度学习的水平。
关键词:以生为本;深度学习;课堂构建
深度学习是课程改革进程中产生的新思想 。那么, 何谓深度学习呢? 它是一种相对的概念,是立足基础知 识所开展的一种更深层次、更广范围、更活思维的学习 模式。其中,思考是深度学习的核心。学生开展深度思考 和探究,从问题表象追寻问题的本质,这是深度学习的 基本形式 。就初中数学学科而言,它是理论性与实践性 相融合的学科,是学生学习其他理论学科的基础 。而数 学学科的理论性极强 ,学生想要真正掌握数学知识,就 必然需要进行深度学习,由此,当前的初中数学教学中, 构建深度学习课堂已成为重要的趋势。
一、“以生为本”理念对深度学习的影响
学生是学习与成长的主体 。随着时代的发展,学生 在学习中的主体地位越来越受到重视。传统的教学理念 是以教师为主体 ,而在实践探索和研究中我们发现,提 高课堂教学质量的关键在于学生而不在于教师。学生主 动学,课堂质量就能够明显提升,由此,“以生为本”的理 念逐渐应用到课堂教学之中。而深度学习就是引导学生 自主思考、自主探索的过程,摆正“以生为本”的观念,将 对深度学习产生重要的影响。
(一)生本理念为深度学习奠定了思想基础
生本理念是充分尊重学生主体地位的理念,它正视 学生在学习中的地位,考虑他们的学习需求,尊重他们 的学习欲望,这就使教学过程有正确的思想依托,教师 认真挖掘学生的需求,并以他们自主探索为核心,这使 得推进深度学习的过程有了充分的思想基础。
(二)生本理念为深度学习明确了教学方向
思想引导行为,生本理念让教师在开展深度学习课 堂教学时有了明确的方向,能够充分遵循学生的学习需 求,用更加契合学生发展的教育方式引领学生的学习活动,培养他们的思维品质,让课堂更加有目标、有方向, 这是深度学习课堂教学方向得以明确推进的关键。
(三)生本理念为深度学习构筑了有力保障
生本理念不仅是一种教育思想,还是贯彻教学始终 的精神动力 。生本理念下,课堂的任何活动都依据学生 的需求,立足学生的发展,这是人才培养的核心目标。随 着学生的成长 ,他们的深度学习需求会产生不同的变 化,而立足生本理念,课堂教学将随之变化,有效契合, 这就为学生有效地开展深度学习提供了有力的保障。
二、基于“以生为本”理念的初中数学深度学习课堂 的构建策略
数学是初中阶段的重点学科,也是学生以后应用最 广泛的学科 。由此可见,开展数学深度学习对学生的成 长和能力的发展具有十分关键的作用。而数学学科是理 论性很强的学科,诸多理论元素需要学生沉入其中,深 度挖掘 ,如此才能够真正将知识变为自身的能力,所 以,教师应当立足以生为本的理念,通过层递式、渐进 式的方法激活学生的数学思维 ,帮助他们拓展深度学 习之路。
(一)由表及里,用问题激活学生思维
数学思维是深度学习最为重要的组成部分。而数学 学科是注重理论结合实际的学科,在教学实践中,数学 理论的应用通常需要正视问题的本质,由此才能更好地 挖掘解决问题的办法 。这是数学应用的首要条件,也是 学习数学知识所需要培养的思维能力 。所以,问题是激 活学生课堂思维的关键。引导学生通过问题探寻事物本 质,由表象走进内里,了解问题的原因,掌握问题的方 法,这样才能够推动学生更好地理解数学知识,应用数 学原理。因此,深度学习的核心就是问题。教师应当在课堂上活用问题,激发学生的思维,引导他们由表及里地 探寻问题,从而有效地解决问题。
以人教版七年级下册“二元一次方程组”的教学为例 ,二元一次方程组是生活中应用较广泛的数学知识, 有时候运用方程组去解决实际问题,会比用直接推断的 方式更便捷。而二元一次方程组的应用通常都不是独立 出现的,必然与其他知识相关联,在这种情况下,教师就 要灵活地用问题去激活学生的思维,让他们更加迅速地 把握问题的本质。以综合运用问题为例:如果三角形的 三个内角分别是 x°,y°,y° ,求:(1)x,y 满足的关系式; (2)当 x=90 时,y 的值;(3)当 y=60 时,x 的值。此时结合 条件,教师可以提出问题:根据已知条件,可以知道这个 三角形是什么三角形? 学生不难发现,三角形的两个内 角相等,由此可以推断出该三角形是等腰三角形 。而在 此基础上,学生很容易列出相应的关系式:x+2y=180,继 而结合具体的 x 值和 y 值 ,就能够求得相应的未知数。 此时教师还可以再提出问题:如果增加已知条件“x=2y”, 那么你能直接求得 x 和 y 的值吗? 根据这个问题,学生 会进行发散性思考,结合三角形内角和的原理,并尝试 运用二元一次方程组的求解方法 ,从而解得 x=90,y= 45,即该三角形为等腰直角三角形。在解题过程中,学生 不仅要运用三角形的知识发散思考相应的特点,同时还 要结合二元一次方程组的解法 ,最终确定问题的本质。 这是一种由表及里的思维模式,学生能够透过现象看到 本质,更加能够运用科学、合理的方法解决实际的问题, 从而不断提升自己的思维水平。
(二)由浅入深,以情境推动学生思考
思考是推动深度学习的关键途径。任何深入的理解 性活动都需要依赖思考来完成 。而数学学科是理论性 很强的学科,包含诸多原理和知识,由此,学生在学习 过程中经常会感到枯燥、晦涩,继而逐步失去思考的动 力,甚至丧失学习兴趣 。这反而降低了深度学习实现 的可能性 。 由此,激活课堂,让学生感受到课堂的乐 趣,是推进深度学习的重要依据 。而数学情境是增强 课堂趣味性、引导学生积极探索的有效手段,教师在 日常教学时可以依据不同的教学情境由浅入深地引 导学生去体验和探索,感受数学理论的内涵,体会数学原理的应用,从而激发他们更加主动地思考,不断地推 动深度学习过程。
以“平面直角坐标系”的教学为例,平面直角坐标系无论是在现实还是在理论中都具有广泛的应用性。借助平面直角坐标,我们能够解决很多有关方向、距离的问题。这是一个具有综合性的知识点。如实际问题:在一次 航海中,有一艘船遇险,救生船通过雷达确定了遇险船的相对位置:北偏东60°,35 n mile 。同时有一位落水者 恰好位于救生船正北方与遇险船正西方的交叉点上。已 知救生船速 5 n mile,不考虑水流速度,请问救生船需 要多久才能够到达遇险船的位置?这个问题是非常常见 的平面直角坐标系的应用问题。在解决这个问题的过程 中,学生需要明确落水者的具体位置,而后还要综合分 析,以确定救援顺序。此时教师可以创设演示情境,用多 媒体等技术工具展示出落水者、遇险船、救生船的相对 位置 。学生能够直观地看出这三者构成了一个锐角为 60°的直角三角形,由此,进一步思考就可以顺利得出救 生艇去救援落水者的时间是 35×cos60°/5=3.5(小时) ,而 由落水者处至遇险船处需要 35×sin60°/5≈6.062(小时) , 合计需 9.562 小时。在解决该问题的过程中,利用情境, 学生能够很直观地建立三个点的位置关系,同时还能够 利用平面直角坐标系的相应知识解决距离问题和时间 问题等。在情境中,学生的思维从抽象到形象、由平面到 立体,他们在思考的过程中,思维就能够由浅入深,逐渐 发现解决问题的核心手段,从而实现深度学习。
(三)由近及远,以探究提高学习能力
深度学习不仅是引导学生深入探索知识的活动,它 的关键的目标是引导学生学会自主学习,掌握有效的学 习方法 ,这样才能够让学生的学习之路更加开阔和深 远 。由此可见,深度学习还需要以培养学生的学习能力 为目标 。而探究活动具有一定的开放性和自主性,能够 让学生充分开阔思维 ,让学习能力在探究中有所进步。 所以,日常教学中教师还需要利用探究活动让学生从眼 前的问题出发,由近及远地去推演、判断,通过推导、归 纳等手段获得解决问题的关键能力,懂得数学学习的方 法,从而不断提升数学学习能力。
以八年级下册“勾股定理”的教学为例,勾股定理是 非常有哲学意义的数学定理,它不仅是数学知识中最为 重要的定理之一,同时也是数形结合的关键纽带,在现 实生活中有极其广泛的应用。勾股定理的现实应用意义 强,学生需要更加灵活地应用和掌握。因此,教师就要带领学生去深度挖掘。教师可以创设合作探究活动,如:一 个门框长 2 m,宽 1 m,一块长 3 m,宽 2.2 m 的长方形 薄木板能否从门框内通过?为什么? 这是一个以勾股定 理为基础的探究问题,在探究过程中,学生从经验出发 初步判断很有可能认为无法通过,而此时追寻为什么的 目标促使他们进行验证、推导、归纳 。由此,学生就会开 展一系列的推演,如木板横着过、竖着过,这种情况都很 快被否决。继而学生就会再思考,木板能不能斜着过呢?
而后利用勾股定理计算,门框的对角线长 ■5 m,约等 于 2.236 m,比薄木板的宽长。基于此,学生就能够顺利 得出木板通过门框的方法。在探究活动中,教师不预先 告知学生用何种方法,而是通过学生的自主探索和思考 去试错和排除 ,继而寻找到最合适的方法去解决问题。 这是引导学生自主学习的活动过程,学生在活动中对勾 股定理的应用更加明晰,从而有效地获得探索理论知识 的能力,逐步增强自己的学习水平。
(四)由偏至全,以总结构建知识体系
深度学习是从片面走向全面的学习模式。在深度学 习之中,学生要看得更多、看得更远,这样才能够真正形 成强有力的知识体系,掌握更加综合的数学能力 。而适 时的总结是推动学生建立健全知识体系的关键,总结是 思考行为的最终导向,也是凝练知识结构与知识体系的 核心路径。借助总结,学生能够更为全面地看待结果,继 而思考过程,从而构建更多维度的知识框架。因此,教师应当有效地利用总结帮助学生及时地反思和审视,使学 习过程由偏至全,更好地搭建起数学知识框架,完善数 学体系。
以八年级下册“平行四边形”的教学为例,平行四边形是常见的四边形之一,它的特点能够很好地应用在几何问题之中 ,尤其在几何证明题中具有非常重要的作 用。而平行四边形涉及哪些特点?分别有什么样的应用? 指向或者关联哪些几何问题?这些都是学生建立几何知 识体系时需要了解的。由此教师可以引导学生运用思维 导图工具在探究时及时进行总结 ,从而不断细化知识 网,完善体系建构。以下题为例:如下图,AB=DC=EF, AD=BC,DE=CF,图中有哪些互相平行的线段?该问题是综合运用平行四边形相应定理的活动,学生结合平行 四边形的判定定理 ,可以很顺利地得出 AB/DC/EF, AD/BC,DE/CF。在此过程中,教师可以引导学生利用 思维导图,以平行四边形为中心,发散式地列举它的性 质。如两组对边分别相等、两组对边分别平行、两组对角 分别相等、对角线互相平分、一组对边平行且相等等,作为第二层级,而后再向外辐射,画出第三层级。如两组对 角都是直角时,变为矩形;对角线相互垂直时是菱形;等 等。这样的总结方式由特殊到一般,再到特殊,是一种由 偏至全的思考方法,能够有效帮助学生搭建完整的知识框架,推动深度学习能力的提升。
三、结语
随着课程改革的不断推进,课堂在学生成长中的地 位更加重要。把握住课堂,学生的学习就更加有方向、有 深度、有目标。而学生作为学习的主体,同时也应当是课 堂的主体,是学习活动的关键参与者 。要引导学生更好 地发展,就必然要正视他们的地位,鼓励他们通过深度 学习去探索和实践 ,在深入挖掘和探寻中提升能力、开 阔思维,更好地掌握知识。
初中阶段是学生转向高阶学习的关键阶段,教师应 当充分立足生本理念,尝试引导学生积极投入,更加积 极主动地探索数学奥秘,从而构建起有效的深度学习课堂,推动学生的长远发展。
参考文献:
[1]罗兵,方荣雁,戴希.基于深度学习的初中数学课堂教学 问题设计实践与思考[J] .湖州师范学院学报,2021(4) :113- 115.
[2]马玉慧,夏雪莹,张文慧.基于深度学习的教师课堂提问 分析方法研究[J] . 电化教育研究,2021(9) :108- 113.
[3]陆佳龙.有效引导,促进数学课堂教学中的深度学习[J] . 教育观察,2020(15) :59-60.
[4]范生娜.深度学习理论下初中数学单元主题作业设计与 实践:以《线段的最值》为例[J] .福建教育学院学报,2021(6) :25- 26.